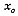 without a measurement, such as a water
table elevation at a site where there is no well. Kriging produces an estimate
without a measurement, such as a water
table elevation at a site where there is no well. Kriging produces an estimate
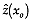 as a linear combination of
k observations
as a linear combination of
k observations 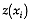 around
around
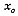 :
:
Acquisition Activity, Statistical Quality Control, and Spatial Quality Control for 1997 Annual Water Level Data Acquired by the Kansas Geological Survey
Prev Page--Statistical Quality Control Measurements || Next Page--Conclusions
The previous statistical analysis of quality control was done without directly taking into consideration the mutual distances among points defined by the penetration of the water table by a well.
Spatial location of water table at any given well is given by two Cartesian coordinates and the elevation of the water table above sea level, neither of which has been traditionally measured directly. Until last year, Cartesian coordinates have been derived from latitude and longitude, which in turn are a numerical transformation of the legal description of the location of the well. The Kansas Geological Survey (KGS) has just started to employ satellite Global Positioning System (GPS) to determine latitude and longitude in those wells previously measured by the United States Geological Survey.
A second source of error derives from the fact that what is actually measured is the depth to the water table. The elevation is calculated by subtracting depth to water from the surface elevation, which has never been measured directly. In a state with at most rolling hills, the conventional wisdom has been that one can obtain the elevation of any well with reasonable accuracy by locating the well on the appropriate 7 1/2 minute topographic map produced by the United States Geological Survey and reading the elevation by interpolation from the contour lines. The scale of these maps is 1:24,000 and the contouring interval is generally 10 ft.
Common sense and the physics of fluid flow indicate that water table elevation of a given aquifer should vary continuously in a way that wells nearby should have similar water table elevations, similarity that should deteriorate with distance in a systematic fashion. Under that assumption, the applications of the probabilistic models of geostatistics are helpful to verify if the data comply with the assumptions. The analysis will be limited to wells supposedly tapping the High Plains aquifer, the only aquifer in the state with a sampling density regular and high enough to apply geostatistics.
Methodology
Geostatistics has several estimation methods--generically known by the name of
kriging--that are able to estimate the value of an attribute at a location
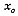 without a measurement, such as a water
table elevation at a site where there is no well. Kriging produces an estimate
without a measurement, such as a water
table elevation at a site where there is no well. Kriging produces an estimate
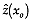 as a linear combination of
k observations
as a linear combination of
k observations 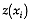 around
around
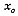 :
:

 are weights that come from the
solution of a system of equations (Journel and Huijbregts, 1978). The following
figure illustrates the case of a sample of size 6 in which
are weights that come from the
solution of a system of equations (Journel and Huijbregts, 1978). The following
figure illustrates the case of a sample of size 6 in which
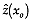 = 3149.6.
= 3149.6.
Figure 1--Kriging estimation for a sample involving six wells. A solid dot
denotes a well location and the labels are, from top to bottom, water table
elevation, in feet, and the kriging weight. The question mark shows the
estimation location.
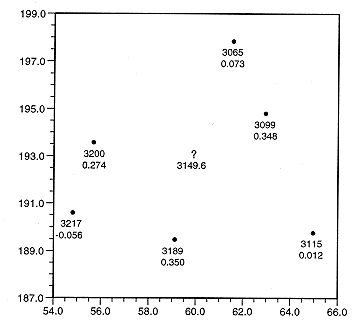
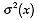 , which
one can use to assess the estimation reliability. The smaller the kriging
variance, the more reliable the estimate.
, which
one can use to assess the estimation reliability. The smaller the kriging
variance, the more reliable the estimate.
Crossvalidation is an ingenious application of kriging for the verification of parameter selections necessary for the solution of the system of equations. Here, instead, crossvalidation is employed to check the spatial consistency of the data. Given a sample of size n, each observation is dropped in turn, and for each discarded observation, an estimate is computed at the location of the discarded observation by using at most the remaining (n - 1) measurements. By pretending that an observation was never taken, one can genuinely produce an estimate at the location, and by bringing it back, a kriging estimation error can be computed by comparison with the true value.
Kriging is the best linear unbiased estimator. Even so, like any of the rest of the spatial estimation methods, it is not perfect, in the sense that crossvalidation errors are not zero. However, under normal circumstances, the discrepancies stay below two kriging standard deviations. Otherwise, the measurement could be either an anomaly or an observation in error. Close scrutiny is the only way to differentiate between the two, but considering suspect observations are commonly a small fraction of the sampling, when examining the accuracy of a sampling it is always less time consuming to restrict the attention to observations flagged by crossvalidation than to re-examine the entire data set.
Given that a high estimation error could be produced by poor sampling control,
it is more convenient to analyze z scores 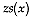 ,
which is the kriging estimation error over its standard deviation
,
which is the kriging estimation error over its standard deviation
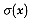

Crossvalidation of a first version of the 1997 measurements
The Kansas Geological Survey measured 437 wells last January that were coded as being screened within the High Planes aquifer by the KGS Geohydrology Section. The KGS Exploration Services Section carefully inspected all measurements before sending them for spatial analysis.
Because the minimum resolution of the legal description of well locations has a precision of 10 acres, wells closer than 1/8 of a mile sometimes have the same legal description, which results in the same latitude and longitude and Cartesian coordinates, despite the fact the wells are close but not really at the same spot. Kriging cannot handle multiple observations per site for the same attribute. One well was discarded from each of three pairs of wells with the same coordinates. In all cases, the water table elevations per pair were very similar, so the discarding took nothing away from the generality of the analysis.
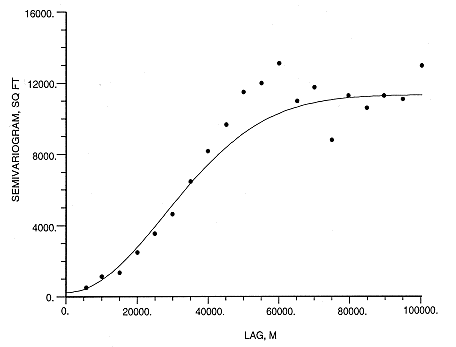
Calculation of kriging weights and kriging variance depends on several parameters. But none is as crucial as the semivariogram, which is a function related to the degree of spatial continuity of the model. The prevailing practice is to estimate the semivariogram at discrete distances and then fit admissible models, such as the Gaussian model shown in the figure. Axi "admissible" model is one that assures a unique solution to the kriging system of equations and a positive kriging variance.
Figure 2--Semivariogram model for the original sampling in the N2W average
direction of the trend strike. The model is Gaussian, with a nugget of 426.3 sq
ft, an effective range of 76594.3 meters and (sill-nugget) equal to 13355.5 sq
ft.
The following table and map summarize the results for the crossvalidation of the 1997 original sampling. Both the USGS and the KGS well names are too long for posting, so the map and table use an arbitrary sequential number for labeling.
| Original sampling z-scores larger than two and ordered by increasing z-score | ||||||
|---|---|---|---|---|---|---|
| No. | USGSID | KGS ID | Easting (m) | Northing (m) | WTE (ft) | Z-score |
| 320 | 373223099472101 | 29S 23W 12BAC 01 | 430253.6 | 4154832.8 | 2263.56 | -4.48 |
| 284 | 374255101251501 | 27S 38W 12ADC 01 | 286599.6 | 4176727.2 | 2868.14 | -2.82 |
| 308 | 373607100565301 | 28S 33W 20ACD 01 | 327859.2 | 4162901.2 | 2595.37 | -2.27 |
| 309 | 373632101004301 | 28S 34W 14CCC 01 | 322281.1 | 4163957.8 | 2630.22 | -2.25 |
| 127 | 380622101014001 | 22S 34W 26CCC 01 | 322072.7 | 4219233.0 | 2768.26 | -2.24 |
| 373 | 372016101201201 | 31S 37W 22BCC 01 | 292780.8 | 4134592.2 | 2837.50 | -2.15 |
| 101 | 382159098545001 | 19S 14W 30CDD 01 | 507439.3 | 4245866.5 | 1840.35 | -2.10 |
| 370 | 372128101065001 | 31S 35W 15BAA 01 | 312836.0 | 4136575.2 | 2703.44 | -2.07 |
| 406 | 370931101280201 | 33S 38W 2ODDB 01 | 280806.4 | 4115182.5 | 3029.64 | -2.04 |
| 328 | 372942100192201 | 29S 27W 3OBCC 01 | 383145.6 | 4150575.8 | 2500.61 | -2.03 |
| 206 | 375226100564601 | 25S 33W 16DCC 01 | 328753.6 | 4193353.0 | 2828.85 | 2.28 |
| 371 | 372227101121501 | 31S 36W 02CDD 01 | 304726.1 | 4138357.0 | 2827.18 | 2.55 |
| 377 | 371425100272002 | 32S 29W 27AAB 02 | 370766.7 | 4122452.8 | 2529.22 | 2.63 |
| 248 | 374638101495001 | 26S 41W 2OBCD 01 | 250753.2 | 4184441.8 | 3270.62 | 2.75 |
| 202 | 375436100561301 | 25S 33W 03BCC 01 | 329640.9 | 4197381.5 | 2847.49 | 3.04 |
| 220 | 375149101341601 | 25S 39W 23BDD 01 | 273914.1 | 4193726.0 | 3197.25 | 3.16 |
| 247 | 374917101242701 | 26S 37W 06ACB 01 | 288193.9 | 4188306.0 | 3066.18 | 3.55 |
| 391 | 371654101244001 | 32S 38W I 1ADA 01 | 300752.0 | 4115375.5 | 3014.83 | 4.79 |
| 178 | 375732100363002 | 24S 3OW 15CCC 02 | 379636.2 | 4159130.8 | 2693.81 | 5.59 |
| 379 | 371733100402001 | 32S 3 IW 03DAA 01 | 351536.7 | 4128524.5 | 2729.13 | 7.08 |
Despite the careful handling of the data, in absolute value the highest four z-scores are due to errors in data preparation:
Finally a well-by-well check of the 7 1/2 minute topographic maps of surface elevation for all wells with a z-score above 2.0 disclosed that well 101 was also in error. The surface elevation should be 1905 ft instead of 1875 ft.
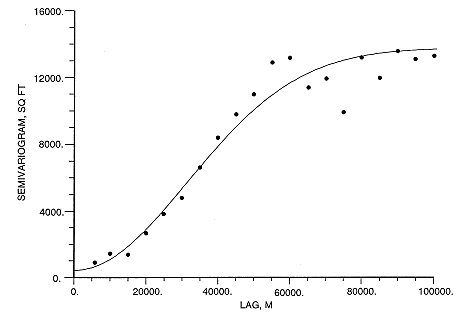
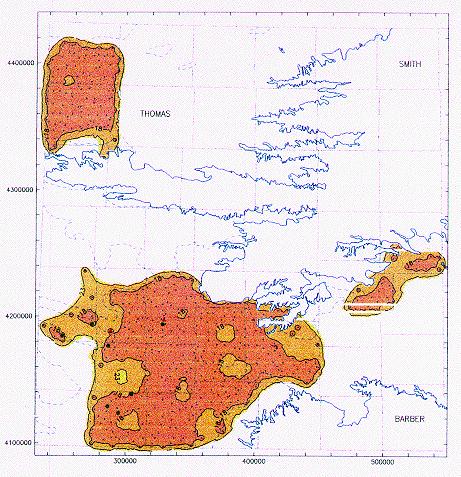
Figure 3--Coded posting of z-scores for the original sampling.
A cross denotes a well with a z-score below 2; a red dot, between 2 and 3; and a red
triangle, larger than 3. The solid blue line is the actual boundary of the High
Plains aquifer and the segmented line the boundary of its non-contributing
portion. A larger version of this figure is available.
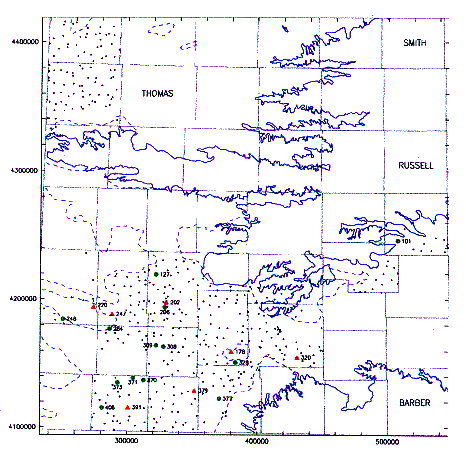
Figure 4--Universal kriging estimation of water table
elevation employing the original sampling. A cross denotes a well with a z-score
below 2; a red dot, between 2 and 3, and a red triangle larger than 3. The solid
blue line is the actual boundary of the High Plains aquifer and the segmented
line the boundary of its non-contributing
portion. A larger version of this figure is available.
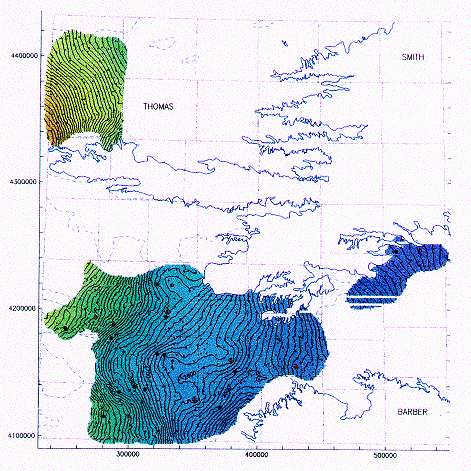
Figure 5--Southwestern Kansas enlargement of a universal
kriging estimation of water table elevation employing the original sampling. A
cross denotes a well with a z-score below 2; a red dot, between 2 and 3; and a
red triangle, larger than 3. The solid blue line is the actual boundary of the
High Plains aquifer and the segmented line the boundary of its non-contributing
portion. A larger version of this figure is available.

Edited version of the 1997 measurements
The semivariogram is half the mean-square difference in the attribute for
locations separated by the same distance along the same direction. Modeling of
the semivariogram is not totally insensitive to the errors detected by
crossvalidation. Away from the wells in error, changes are minor in terms of the
effects on the estimate 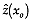 ,
but the kriging variance has an important global
reduction in accordance with the better continuity implied but the disappearance
of the sudden fluctuations associated to the wells in error. Such reduction in
,
but the kriging variance has an important global
reduction in accordance with the better continuity implied but the disappearance
of the sudden fluctuations associated to the wells in error. Such reduction in
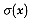 makes the z-scores in (2) to
increase even if the kriging error
makes the z-scores in (2) to
increase even if the kriging error 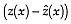 remains the same.
remains the same.
Figure 6--Semivariogram model for the edited sampling
in the NS average direction of the trend strike. The model is Gaussian, with a
nugget of 240.6 sq ft, an effective range of 67868.4 meters and (sill-nugget)
equal to 11102 sq ft.
| Edited sampling z-scores larger than three and ordered by increasing z-score | ||||||
|---|---|---|---|---|---|---|
| No. | USGSID | KGS ID | Easting (m) | Northing (m) |
WTE (ft) | Z-score |
| 284 | 374255101251501 | 27S 38W 12ADC 01 | 286599.6 | 4176727.2 | 2868.14 | -3.69 |
| 390 | 371420101185501 | 32S 37W 26BAC 01 | 294566.0 | 4123666.5 | 2985.44 | 3.07 |
| 391 | 371654101244001 | 32S 38W I 1ADA 01 | 286112.6 | 4128743.0 | 3014.83 | 3.19 |
| 371 | 372227101121501 | 3 IS 36W 02CDD 01 | 304726.1 | 4138357.0 | 2827.18 | 3.48 |
| 220 | 375149101341601 | 25S 39W 23BDD 01 | 273914.1 | 4193726.0 | 3197.25 | 3.53 |
| 248 | 374638101495001 | 26S 41W 2OBCD 01 | 250753.2 | 4184441.8 | 3270.62 | 3.54 |
| 206 | 375226100564601 | 25S 33W 16DCC 01 | 328753.6 | 4193353.0 | 2828.85 | 3.80 |
| 247 | 374917101242701 | 26S 37W 06ACB 01 | 288193.9 | 4188306.0 | 3066.18 | 4.54 |
| 202 | 375436100561301 | 25S 33W 03BCC 01 | 329640.9 | 4197381.5 | 2847.49 | 5.11 |
In this case one can see that correction of only five errors has an important influence on the estimation of the water table elevation. Coding of z-scores has been changed to compensate for the effect produced by the change in semivariogram model. At this stage it is safe to say that all wells with high z- scores have correct Cartesian coordinates, surface elevations and depth to the water table. Further scrutiny of a more geohydrologic nature is recommended to discard other more natural but equally disturbing causes, such as tapping aquifers other than the High Plains aquifer.
Figure 7--Universal kriging estimation of water table
elevation employing the edited sampling. A cross denotes a well with a z-score
below 2; a red dot, between 2 and 3, and a red triangle larger than 3. The solid
blue line is the actual boundary of the High Plains aquifer and the segmented
line the boundary of its non-contributing
portion. A larger version of this figure is available.
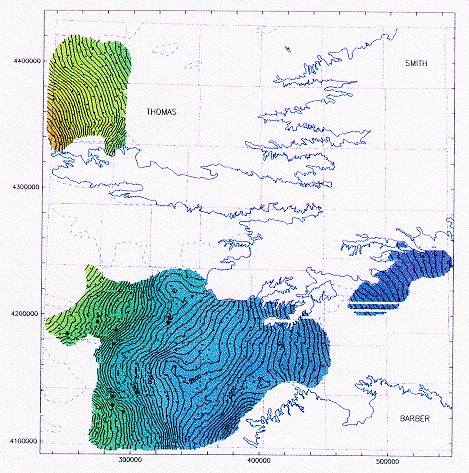
Figure 8--Southwestern Kansas enlargement of a universal
kriging estimation of water
table elevation employing the edited sampling. A cross denotes a well with a
z-score below 3; a red dot, between 3 and 4; and a red triangle, larger than 4.
The solid blue line is the actual boundary of the High Plains aquifer and the
segmented line the boundary of its non-contributing portion.
A larger version of this figure is available.
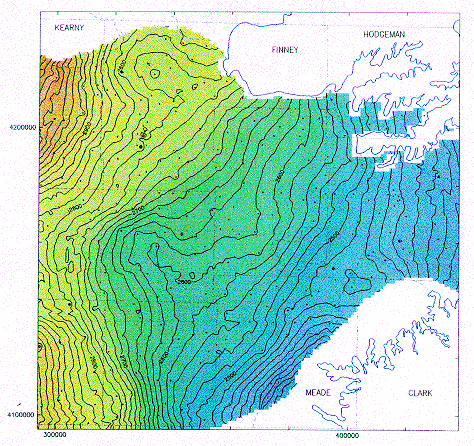
Figure 9--Universal kriging standard deviation for the
edited sampling. A cross
denotes a well with a z-score below 3; a red dot, between 3 and 4; and a red
triangle, larger than 4. The solid blue line is the actual boundary of the High
Plains aquifer and the segmented line the boundary of its non-
contributing portion.
A larger version of this figure is available.
Conclusions
Perfect editing of large data bases is tedious, time consuming, and laborious, thus expensive.
In the specific case of the High Plains Observation Network, five important errors escaped detection by the numerous and serious editing efforts of the United States Geological Survey, the KGS Geohydrology Section, and more recently by the KGS Exploration Services Section.
Crossvalidation is an inexpensive and fast spatial quality control tool to run. It works by restricting attention to measurements with high z-scores. Although true geological anomalies also lead to high z-scores, sometime high z-scores are produced by inconsistencies in the sampling. Given that the proportion of observations with z-scores over 2.0 are small, a ranking of the observations by z-scores is cost effective because of the significant reduction in the number of measurements, calculations, and transcriptions that must be reviewed.
The Kansas Geological Survey should further investigate wells still posting high z-scores to discard anomalous sources of variations such as misclassification of wells into the High Plains aquifer category.
As a by-product, the kriging standard deviation map suggests that a few more wells in areas with high kriging standard deviation will add significant reliability to the estimation of the water table elevation.
References
Journel, A. G. and C. J. Huijbregts, 1978, Mining Geostatistics: Academic Press, London, England, 600 p.
Putnam, J. E., D. L. Lacock, D. R. Schneider, M. D. Carlson, and B. J. Dague, 1996, Water Resources Data-Kansas, Water Year 1995, 488 p.
Prev Page--Statistical Quality Control Measurements || Next Page--Conclusions