Kansas Geological Survey, Open File Report 96-50
Although the grid of 2-D seismic data in the Minneola complex has been successfully used to identify at least the thicker Pennsylvanian drainage channels (Clark, 1987, 1995; Fig. 3), it has not been successful in determining whether these channels contain productive sandstones, or are filled with shale and other non-productive units. Part of the reason for this may be the lack of higher frequencies in the data necessary to identify possible differences in seismic amplitude and isochron anomalies between shale-filled channels (or those with other non-productive units) and those containing potentially productive Morrowan sandstones. Most of the seismic data acquired over the Minneola complex never recorded, or do not contain usable frequencies above 100 Hz. Without those higher frequencies, it may be difficult, if not impossible, to distinguish a shale filled channel with one containing a potentially productive 15 ft. (5 m) or thinner sandstone. Although full wavelength resolution of a 15 ft sandstone at a depth of 5000 ft. or more is unlikely, it is possible that high-resolution seismic data which contains frequencies above those previously acquired could be affected enough by a thin sandstone such as this to yield a different seismic signature than a channel fill interval that does not contain a productive sandstone.
One way to inexpensively test the above hypothesis is by the generation of synthetic seismic models from sonic and density logs in the Minneola complex. Although the models generated with this method will not contain diffractions and do not take into account other factors such as ray path distortions, spherical divergence, anelastic attenuation, freznel zone affects, multiples, and excessive random or coherent noise, it will give an idea as to what the seismic response of a measured geologic interval should be on a vertically incident seismic trace with a given frequency bandwidth and phase type.
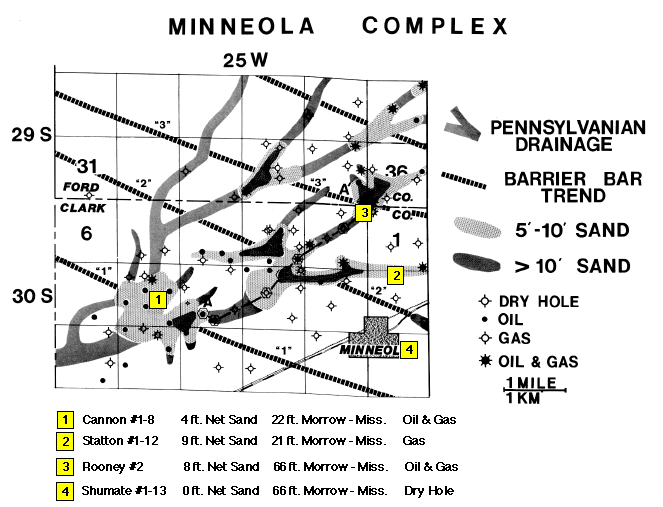
The wells used in the modeling are shown as yellow squares in Figure 3. Not all of the wells in the field contain sonic and bulk density logs. The wells chosen contain both in order to determine accurate acoustic impedance contrasts. The Cannon #1-8 well was chosen to represent a relatively thin Morrow-Mississippian interval (22 ft.; 6.7 m.) with a relatively thin net sand thickness in the upper part of the section (4 ft.; 1.2 m.). The Statton #1-12 well contains almost the same Morrow-Mississippian interval as the Cannon well but contains twice as much net sand (9 ft.; 2.7 m.). Although this is not the thickest net sand penetrated in a well, it is the thickest in which both sonic and density logs are available. The change in seismic signature between these two wells should indicate the feasibility of seismicly determining a relatively medium thickness Morrow sand from a much thinner one when the channel fill is relatively thin. The Rooney #2 well contains approximately the same net sand thickness as the Statton well (8 ft; 2.4 m.), but contains a thicker Morrow-Mississippian interval (66 ft.; 20 m.) representative of a thicker channel fill. Difference in the seismic signature between the Statton and Rooney wells will indicate what to expect when a channel fill interval thickens but the net sand thickness remains the same. The Shumate #1-13 well was chosen to represent a thicker Morrow-Mississippian interval that is completely filled with shale and other nonproductive units. Comparison between the Shumate and Rooney wells should indicate what seismic signature differences can be expected between a relatively moderate to thick channel sequence that contains a potentially productive upper Morrow sand and one that does not.
Figure 3--Wells used in seismic modeling (yellow squares). Base map of the Minneola complex indicates well locations, major lower Pennsylvanian drainages as interpreted from previously acquired seismic data, and barrier bar sandstone accumulations and trends mapped from well control (modified from Clark, 1987).

All of the models were generated using automatic log interpolation between the actual well control points. The interpolation was constrained between correlation horizons (tops) which were manually picked on each well, and the log values at each well. By using both the sonic and density logs, interpolated acoustic impedance log models with vertical sampling intervals of 1 ft. (0.3 m) were generated. These models contained a trace at each well and 19 interpolated traces between wells. Zero phase, normal polarity Ricker wavelets, with bandwidths determined by Ormsby bandpass filters, were convolved with every trace of the interpolated log models. This process resulted in synthetic seismic models that are similar to migrated, stacked, zero phase seismic sections. In the simplest case, a peak would indicate an increase in seismic impedance downward, whereas a trough would indicate a decrease in seismic impedance downward. Because of the zero phase nature of the wavelet, these peaks and troughs would be centered at the change in impedance. However, due to bandwidth limitations, and the occurrence of many impedance contrasts throughout the stratigraphic section, the actual seismic signature is the result of a combination of many reflections, some higher amplitude than others, that occur from each change in acoustic impedance. These individual reflections interact with one another to form a relatively complex seismic trace.
Two log interpolation models were generated. The single well model uses only the Statton well and modified versions of the sonic and density logs to create a pseudo-geologic cross section in which only the Morrow-Mississippian interval varies. This eliminates any seismic signature change due to changes in lithology or thickness outside the interval of interest and makes interpretation of the resulting seismic anomalies less complex. The multi-well model uses different wells to create a pseudo-cross section. Although the seismic signature differences between these wells may represent a more realistic picture, differences in lithology and thicknesses in units outside the interval of interest may complicate the interpretation.
Two versions of both the single well and multi-well models were generated. A lower resolution model was generated with a frequency bandwidth that approximates the average bandwidth of previously gathered conventional seismic data in the Minneola complex. The bandwidth for this model ranges from 20-30 Hz on the low end and 60-90 Hz on the high end. The lower resolution model would indicate anomalies that could possibly be seen on existing seismic data. A higher resolution model was also generated with a frequency bandwidth that could be expected with a seismic survey designed for high-resolution imaging. The bandwidth for this model ranges from 20-30 Hz on the low end (same as the lower frequency model) and 120-180 Hz on the high end. The high end of the higher resolution model represents a gain of one full octave over the lower resolution model. This amount of increase results in a considerably higher resolution wavelet that has much better definition between the central peak and adjacent side-lobes. Two plots of each of the lower and higher resolution models are also shown, one without random noise, and one with 10% random noise added to make the synthetic seismic section look more realistic, and to determine the sensitivity of the seismic anomalies to random noise.
In all the models, figures of the cross sections, interpolated well log models, and synthetic seismic models are shown in color. For black and white versions of the interpolated log model figures, or a black and white versions of the synthetic seismic model figures with every 2nd variable area-wiggle trace shown instead of every 4th trace as in the colored versions, see Appendix A. The figure numbers for the black and white versions are the same as the colored versions but with an "A" prefix before the figure number (e.g. A4b).