When the upper media boundary is water instead of air the generated seismic surface waves known as Scholte instead of Rayleigh waves. Underwater MASW (Ivanov et al., 2000; Kaufmann et al., 2005; Park et al., 2005) data acquisition and Scholte-wave processing steps are similar to the Rayleigh-wave MASW. However, proper adjustments to data-acquisition equipment and mathematical apparatus are required.
1. Acquiring Scholte-wave MASW records
Underwater MASW data acquisition can be performed using an air-gun source and hydrophone receivers (Figure 1).
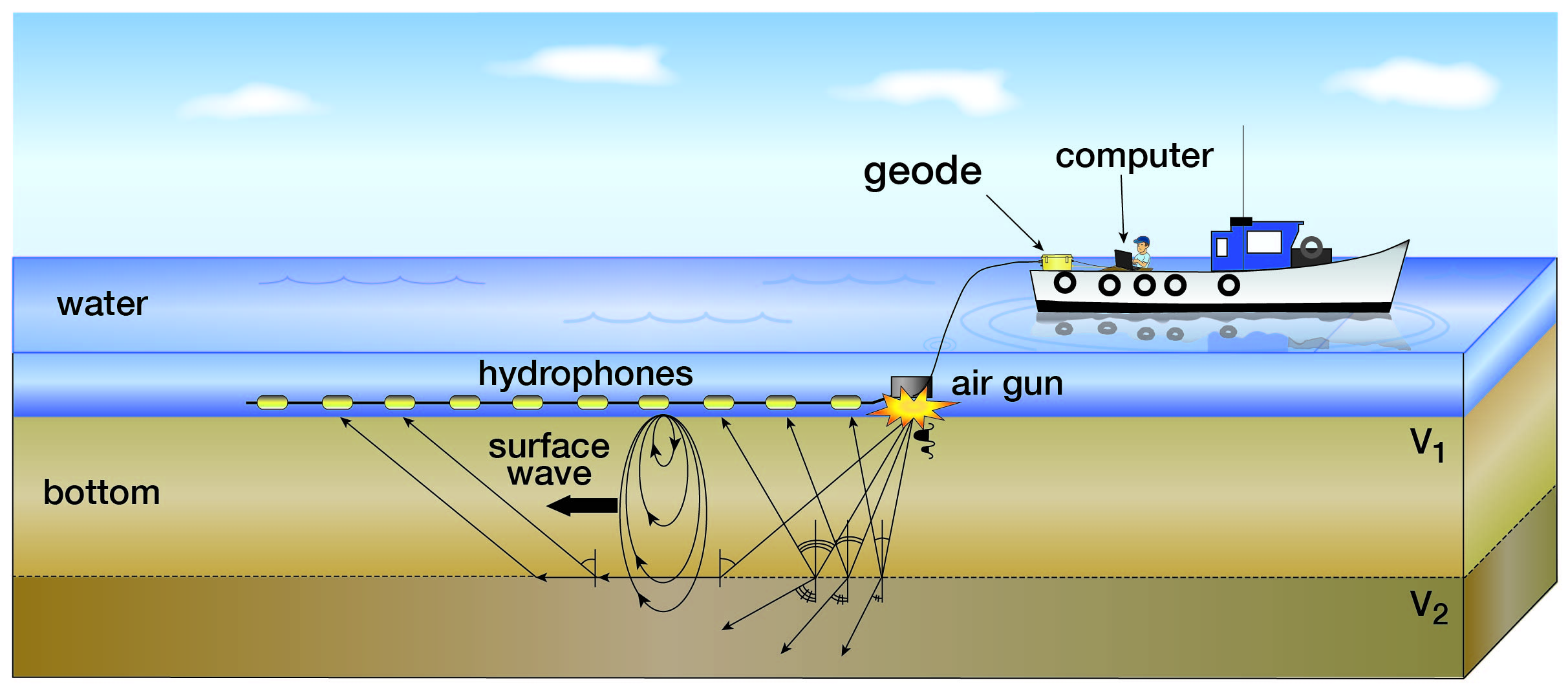
Figure 1. Active underwater MASW data acquisition diagram showing a boat with a seismograph (e.g., Geode) and a computer on board tagging a cable with a stream of hydrophone receivers and using an air-gun seismic source.
2. Processing Scholte-wave data
Scholte-wave processing is identical to the Rayleigh wave except for the forward modeling and inversion components. SurfSeis provides unique mathematical tune ups using water-layer thickness, density and velocity information. Scholte-wave processing results have been verified by comparing Scholte-wave dispersion-curve modeling calculations with synthetic seismic-data forward modeling (Zeng et al., 2012) dispersion-curve images.
References
Ivanov, J., C. B. Park, R. D. Miller, J. Xia, J. A. Hunter, R. L. Good, and R. A. Burns, 2000, Joint analysis of surface-wave and refraction events from river-bottom sediments: 70th Annual International Meeting, SEG, Technical Program Expanded Abstracts, 19, 1307-1310.
Kaufmann, R. D., J. H. Xia, R. C. Benson, L. B. Yuhr, D. W. Casto, and C. B. Park, 2005, Evaluation of MASW data acquired with a hydrophone streamer in a shallow marine environment: Journal of Environmental and Engineering Geophysics, 10, 87-98.
Park, C. B., R. D. Miller, J. Xia, J. Ivanov, G. V. Sonnichsen, J. A. Hunter, R. L. Good, R. A. Burns, and H. Christian, 2005, Underwater MASW to evaluate stiffness of water-bottom sediments: The Leading Edge, 24, 724-728.
Zeng, C., J. H. Xia, R. D. Miller, and G. P. Tsoflias, 2012, An improved vacuum formulation for 2D finite-difference modeling of Rayleigh waves including surface topography and internal discontinuities: Geophysics, 77, T1-T9.
